Temperaturverläufe in Speicher-Behältern und Rohrleitungen berechnen

„Wie schnell kühlt sich ein zylindrischer Solarspeicher mit 1,5 m Durchmesser von 80°C auf 40°C ab, dessen Volumen 10 m³ beträgt und der mit einer 100 mm starken Wärmedämmung aus PU-Schaum ummantelt, einer Umgebungstemperatur von 7°C ausgesetzt ist?“ Eine interessante Frage, die auch aus einer Energietechnik-Klausur stammen könnte. Mit deren Beantwortung ließe sich auch klären, welchen Einfluss ein optimiertes A/V-Verhältnis des Speichers auf dessen Temperaturhaltung hat oder was konkret eine Verbesserung der Dämmung bringt.

Fourier-Gleichung für Wärmeleitung
Das hier vorgestellte einfache Excel-Tool greift hierzu auf die Fourier´sche Differenzialgleichung für die Wärmeleitung zurück, um Temperaturverläufe in geschlossenen Systemen wie Behältern oder Rohren bei stehendem Wärmeträgermedium zu bestimmen.
Dabei entspricht die übertragene Wärmeleistung  nach dem Fourier’schen Gesetz für den vereinfachten Fall eines ruhenden Fluids durch eine ebene Wand:

Der Wärmedurchgangskoeffizient entspricht dabei vereinfacht dem Term Lambda/d. Die inneren und äußeren Wärmeübertragungswiderstände werden hierbei ebenso vernachlässigt, wie die Krümmung der Wand, was für dünne Wandstärken sowie große Durchmesser ausreichend genau ist.

Für die Energiebilanz gilt darüber hinaus:



Durch Gleichsetzen der beiden Gleichungen erhält man eine lineare, inhomogene Differenzgleichung 1. Ordnung, mit deren Lösung sowohl die Zeit bis zum Erreichen bestimmter Temperaturwerte, aber auch Temperaturverläufe für beliebige Randbedingungen erstellt werden können. Die Gleichung lautet: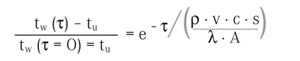



Bei der Verwendung dieser Gleichung muss allerdings einschränkend bemerkt werden, dass diese nur für homogene, isotrope Medien gilt. Also für Medien, die überall gleiche Zusammensetzung haben, sodass die Materialeigenschaften des betrachteten Mediums als ausschließlich von der Temperatur abhängige Größe angenommen werden kann. Darüber hinaus gilt die so formulierte Gleichung auch nur dann, wenn keine Wärme durch Fremdeffekte in den betrachteten Körper eingebracht oder aus ihm entfernt wird (Beladung/Entladung). Das Tool eignet sich daher nicht für Simulationsrechnungen an Speichern, die beispielsweise durch Solarenergie beladen oder im Heizbetrieb entladen werden. Hierzu wäre der Gleichung ein entsprechender Quellterm hinzuzufügen, was die analytische Lösung der Differenzialgleichung aber enorm erschweren würde.

Variantenrechnung für Speicherkonstruktionen
Zurück zur eingangs gestellten Frage nach der Zeitspanne, in der die Temperatur eines 10.000-l-Pufferspeichers von 80°C auf 40°C fällt. Für die zuvor genannten Randbedingungen (Bild 2) ergibt sich ein Wert von etwa 759 Stunden bzw. 31 Tagen. Einen ganzen Monat würde es also dauern, bis die gespeicherte Nutzwärme auf ein, zum direkten Heizen, kaum mehr nutzbares Temperaturniveau fällt. Auf den Ersten Blick ein zufriedenstellender Wert, jedoch bleibt die Frage: Was bringt eine Verbesserung der Wärmedämmung und wie groß ist der Einfluss des A/V-Verhältnisses auf das Abkühlverhalten des Speichers?

Bild 2: Berechnung des Auskühlverhaltens von zylindrischen Pufferspeichern. In welchem Zeitraum fällt die mittlere Temperatur auf einen Zielwert ab?

Hierzu kann mithilfe des Berechnungstools eine Variantenrechnung zur Optimierung der zylindrischen Speicherkonstruktion durchgeführt werden. Im folgenden werden die Abkühlkurven des zuvor genannten  10-m³-Speichers für folgende Varianten gerechnet:

• Speicher 1: 100 mm Wärmedämmung, A/V-Verhältnis 3,0,
• Speicher 2: 200 mm Wärmedämmung, A/V-Verhältnis 3,0,
• Speicher 3: 100 mm Wärmedämmung, A/V-Verhältnis 2,57 (optimal),
• Speicher 4: 200 mm Wärmedämmung, A/V-Verhältnis 2,57 (optimal).

Das Ergebnis: Während es gegenüber Speicher 1 bei Verdopplung der Wärmedämmschicht nur etwa 140 h (18%) länger dauert, bis die Wassertemperatur auf 40°C abfällt (Speicher 2), bringt allein ein optimales A/V-Verhältnis des zylindrischen Speichers (Speicher 3) bereits eine Verlängerung der Abkühldauer um weitere 740 h (97%). Wird ein so konstruierter Speicher darüber hinaus ebenfalls mit einer verdoppelten Dämmschichtdicke versehen, so ergibt sich erst nach 1800 h eine mittlere Temperatur im Speicher von 40°C. Dies entspricht einer Optimierung in Höhe von 137% gegenüber Speicher 1. Eine kurzfristigere Betrachtung der ersten 100 h zeigt, dass sich bereits nach 72 h nennenswerte Temperatur­unterschiede von bis zu 3 K bei den Speichern ergeben (Bild 4).

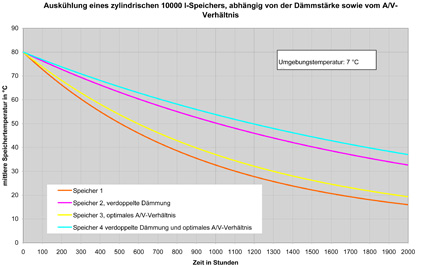
Bild 3: Variantenrechnung – Für Speicher mit gleichem Volumen und variierten A/V-Verhältnissen und Dämmschichtdicken ergeben sich deutliche Unterschiede im Auskühlverhalten.

A/V-Verhältnis optimieren
Daran wird deutlich, dass der wesentliche Optimierungsparameter eines Wärmespeichers dessen A/V-Verhältnis ist. Während die beiden schlanken Speicher 1 und 2 einen Durchmesser von 1,5 m und eine Höhe von 5,66 m aufweisen, beträgt der energetisch optimale Durchmesser für den zylin­drischen 10-m³-Behälter 2,35 m bei ­einer Höhe von nur 2,31 m.
Mit dem Excel-Tool können darüber hinaus beliebige Randbedingungen wie Volumina, Durchmesser und Wärmeleitwiderstände und Schichtdicken für Dämmungen sowie Umgebungstemperaturen und Zieltemperaturen gerechnet werden. Neben einer energetischen Betrachtung von Speicherkonstruktionen kann das Berechnungstool auch für Abkühl- oder Aufwärmprozesse in Rohrleitungen mit stagnierendem Fluid herangezogen werden.

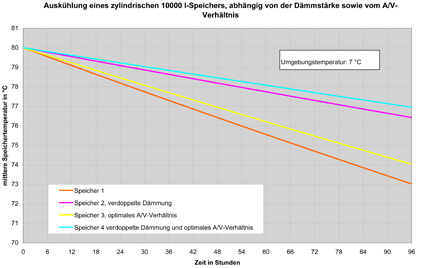
Bild 4: Wie groß ist der Temperaturverlust unterschiedlich konstruierter Speicher innerhalb der ersten 100 Stunden?

Einschätzung der Trinkwassertemperatur bei Stagnation
So z.B. bei der Einschätzung von Trinkwassertemperaturen in Kaltwasserverteilleitungen, bei der ebenfalls mit der oben gezeigten Gleichung zur Wärmeleitung gearbeitet werden kann. Hier stellt sich die Frage, wann bei gegebenen Rohrdimensionen und Dämmstärken die zulässige Maximaltemperatur von 25°C in Kaltwasserleitungen nach DIN EN 806-2 überschritten wird, wenn das in der Rohrleitung stagnierende Trinkwasser gewissen Umgebungstemperaturen ausgesetzt ist. Der Beitrag „Wärmedämmung für Kaltwasserleitungen“ in dieser IKZ-FACHPLANER-Ausgabe beschäftigt sich eingehend mit den hygienischen Aspekten von Fremdwärmeeinflüssen und damit der Wärmeleitungsproblematik in Kaltwasserleitungen. Die darin gezeigten Diagramme zur Bestimmung der Wassertemperatur in Abhängigkeit der Rohrdimension, Dämmstärke und Umgebungstemperatur wurden mit diesem Berechnungstool erstellt.
Das Excel-Tool kann kostenlos von der Internetseite der IKZ-HAUSTECHNIK in der Rubrik „Tool des Monats“ heruntergeladen werden.

www.ikz.de/fachwissen/praxiswissen/marktuebersichten/

MEIN SOFTWARETOOL IM IKZ-FACHPLANER
Verwenden Sie auch selbst erstellte Excel-Tools oder eigene kleine Anwendungsprogramme, die Ihnen den Planungsalltag erleichtern? Möchten Sie Ihr Softwaretool der Fachöffentlichkeit vorstellen? Hier ist der richtige Platz dafür. Schicken Sie uns Ihr Tool mit einer kurzen Beschreibung für das "Tool des Monats" an m.hemmersbach@strobel-verlag.de.