| Ausgabe 7/2005, Seite 6 f. |
Fachmathematik
Einführung in die Fachmathematik
Teil 16: Flächenberechnung Sechseck
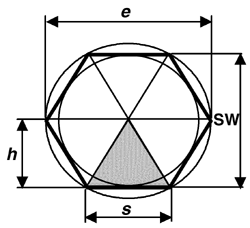
Wird der Mittelpunktswinkel eines Kreises in sechs gleiche Teile aufgeteilt und die Schnittpunkte der Schenkel mit dem Umkreis verbunden, entsteht ein regelmäßiges Sechseck aus sechs gleichseitigen Bestimmungsdreiecken: s = r.
Berechnungsbeispiel 1
Berechnen Sie die Fläche eines regelmäßigen Sechsecks, wenn eine Seite 1 dm lang ist. Das Bestimmungsdreieck ist ein gleichseitiges Dreieck mit 1 dm Seitenlänge.
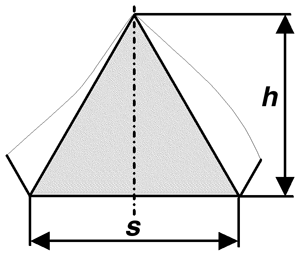
Wertetabelle:
s = 1 dm n = 6
h in dm A in dm2
Lösung:
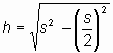
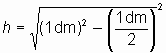
![]()
![]()
A = 2,6 dm2 Sechseckfläche
Erfolgskontrolle:
![]()
![]()
Ergebnis gesichert.
Berechnungsbeispiel 2
Ermitteln Sie aus dem Berechnungsbeispiel 1 das Verhältnis von s und h des Bestimmungsdreiecks von Sechsecken.
Wertetabelle:
s = 1 dm
h = 0,866 dm
Lösung:
![]()
![]()
![]()
Erfolgskontrolle:
Die Verhältniszahlen von s und h gelten für jedes gleichseitige Dreieck.
Ergebnis gesichert.
Deshalb können aus den Berechnungsbeispielen einige für jedes regelmäßige Sechseck typische Verhältniszahlen ermittelt werden:
Radius des Umkreises ra = Seite s |
Radius des Inkreises ri = Höhe h |
Durchmesser des Inkreises di = 2 h |
Durchmesser des Inkreises di = SW |
Durchmesser des Umkreises da = 2 s |
Schlüsselweite SW = 0,866 da |
Durchmesser des Umkreises da = 1,155 SW |
Durchmesser des Umkreises da = Diagonale e |
Fläche A = 2,598 s2 |
Fläche A = 0,649 da2 |
Fläche A = 0,866 di2 = 0,866 [SW]2 |
Berechnungsbeispiel 3
Eine Sechskantschraube mit 14 mm Schlüsselweite soll in ein Hohlprofil versenkt werden. Berechnen Sie den (Mindest-)Durchmesser des Bohrlochs, in das der Schraubenkopf hinein passt.
Wertetabelle:
SW = 14 mm da in mm
Lösung:
da = 1,15 SW = 1,155 14 mm
da = 16,2 mm, gewählt 16,5 mm
Erfolgskontrolle:
![]()
Ergebnis gesichert.
Berechnungsbeispiel 4
Ein kreisrunder Schacht von 80 cm Durchmesser soll eine Schachtabdeckung in Form eines Sechsecks erhalten. Die Abdeckung soll allseits mindestens 10 cm aufliegen. Berechnen Sie die Diagonale e, die Seitenlänge s und die Fläche A der Abdeckung.
Wertetabelle:
d = 0,8 m a = 0,1 m
e und s in m A in m2
Lösung:
e = (d + 2a) 1,155
e = (0,8 m + 2 0,1 m) 1,155
e = 1,155 m
![]()
A = 0,649 e2 = 0,649 (1,155 m)2
A = 0,866 m2
Erfolgskontrolle:
e = 1,155 di = 1,155 1 m
e = 1,155 m
![]()
s = 0,578 m
A = 0,866 di2 = 0,866 (1 dm)2
A = 0,866 m2
Ergebnis gesichert.
Übungsaufgaben
(1)
Berechnen Sie d.
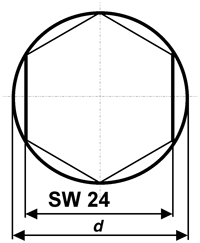
(2)
Ein Schwimmbad in Form eines regelmäßigen Sechsecks hat eine Diagonale (Eckenstrecke) von 5 m. Berechnen Sie die Fläche.
(3)
Für eine Befestigung sollen auf einer Kreislinie 6 Löcher im Abstand von 100 mm gebohrt werden. Bestimmen Sie den Durchmesser des Lochkreises.
© Alle Rechte beim STROBEL VERLAG
