Einführung in die Fachmathematik

Teil 15: Flächenberechnung Kreisring und Ellipse

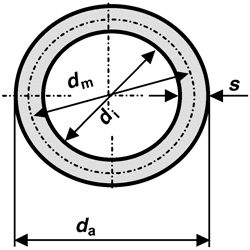
Zwei Kreise mit gleichem Mittelpunkt begrenzen eine Fläche, die Kreisring genannt wird.

Die Kreisringfläche wird berechnet aus der Fläche des Außenkreises, abzüglich der Fläche des Innenkreises.

A = A_a - A_i = d_a² · 0,785 - d_i² · 0,785

A = (d_a² - d_i²) · 0,785

A = s · d_m · 3,14

d_a = 2 d_m - d_i = d_i + 2 s

d_i = 2 d_m - d_a = d_a - 2 s

Berechnungsbeispiel 1

Berechnen Sie für ein Kupferrohr 28 x 1,5 den Strömungs- und den Werkstoffquerschnitt.

Wertetabelle:

d_a = 28 mm   s = 1,5 mm
d_i in mm   A_i und A in mm²

Lösung:

d_i = d_a - 2 s = 28 mm - 2 · 1,5 mm
d_i = 25 mm Innendurchmesser

A_i = d_i² · 0,785 = (25 mm)² · 0,785
A_i = 490 mm² Strömungsquerschnitt

A_a = d_a² · 0,785 = (28 mm)² · 0,785
A_a = 615 mm²

A = A_a - A_i = 615 mm² - 490 mm²
A = 125 mm² Werkstoffquerschnitt

Erfolgskontrolle:

d_m = d_i + s = 25 mm + 1,5 mm
d_m = 26,5 mm

A = s · d_m · 3,14
A = 1,5 mm · 26,5 mm · 3,14
A = 125 mm²

d_i = 2 d_m - d_a = 2 · 26,5 mm - 28 mm
d_i = 25 mm

Ergebnis gesichert.

Berechnungsbeispiel 1.2

Ein Kupferrohr 28 x 1,5 mm soll nach Energieeinsparverordnung mit 30 mm Wärmedämmung ummantelt werden. Berechnen Sie den Dämmstoffquerschnitt in cm².

Wertetabelle:

d_i = 2,8 cm   s = 3 cm
d_a in cm   A in cm²

Lösung:

d_a = d_i + 2 s = 2,8 cm + 2 · 3 cm
d_a = 8,8 cm Dämmstoff-Außendurchmesser
d_m = d_i + s = 2,8 cm + 3 cm = 5,8 cm

A = s · d_m · 3,14
A = 3 cm · 5,8 cm · 3,14 =
A = 55 cm² Dämmstoffquerschnitt

Erfolgskontrolle:

A = (d_a² - d_i²) · 0,785

A = [(8,8 cm)² - (2,8 cm)²] · 0,785

A = [77 cm² - 7,8 cm²] · 0,785

A = 55 cm² (gerundet)

Ergebnis gesichert.

Wird ein Kreis in einer Richtung gestreckt, entsteht eine Ellipse.

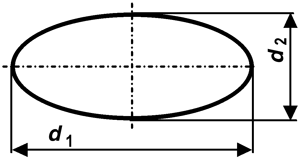
A = d₁ · d₂ · 0,785 = r₁ · r₂ · 3,14

Berechnungsbeispiel 2

Berechnen Sie den Umfang und die elliptische Querschnittsfläche eines Lagerbehälters mit den Abmessungen d₁ = 2,5 m und d₂ = 1,5 m.

Wertetabelle:

d₁ = 2,5 m   d₂ = 1,5 m

l_U in m   A in m²

Lösung:

A = d₁ · d₂ · 0,785
A = 2,5 m · 1,5 m · 0,785
A = 2,94 m² Querschnittsfläche

Erfolgskontrolle:

A = r₁ · r₂ · 3,14

A = 1,25 m · 0,75 m · 3,14 = 2,94 m²

Ergebnis gesichert.

Übungsaufgaben

(1)

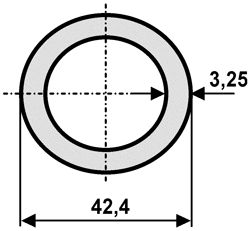
Ein mittelschweres Gewinderohr DN 32 nach DIN 2440 hat 42,4 mm Außendurchmesser und 3,25 mm Wanddicke. Berechnen Sie den Strömungs- und den Werkstoffquerschnitt.

(2)

Ein Kupferrohr 28 x 1,5 mm soll nach Energieeinsparverordnung im Kreuzungsbereich mit 15 mm Dämmstoff ummantelt werden. Berechnen Sie den Dämmstoffquerschnitt in cm².

(3)

Das Tauchbecken einer Saunaanlage hat die Form einer Ellipse. Der Beckenboden hat die Achsmaße 2 m x 1,5 m. Berechnen Sie die Bodenfläche und die Länge des Bodenrandes.

© Alle Rechte beim STROBEL VERLAG