| Ausgabe 4/2005, Seite 10 f. |
Fachmathematik
Einführung in die Fachmathematik
Teil 13: Flächenberechnung Dreieck
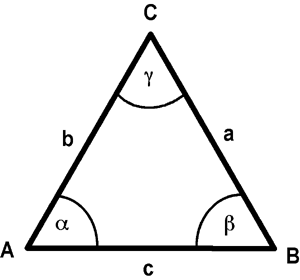
Drei verbundene Punkte einer Ebene, die nicht auf einer Geraden liegen, bilden die Eckpunkte eines Dreiecks. Diese Punkte werden - fachgemäß entgegen der Drehrichtung der Uhrzeiger - mit A, B und C bezeichnet. Die Verbindungen der Eckpunkte sind die Seiten des Dreiecks. Sie werden mit kleinen lateinischen Buchstaben a, b und c bezeichnet, sodass die Seite a gegenüber dem Eckpunkt A; b gegenüber B und c gegenüber C liegt. Jeweils zwei Seiten bilden die Schenkel der Innenwinkel
a, b und g.Der Winkel
a liegt an der Ecke A, b liegt an der Ecke B und g an der Ecke C. Die Summe der Innenwinkel beträgt 180°. Damit ist durch zwei Winkel der dritte bestimmt.Dreiecke werden u.a. eingeteilt:
- nach der Größe der Seiten in gleichseitige, gleichschenklige und ungleichschenklige Dreiecke,
- nach der Größe der Winkel in spitzwinklige, rechtwinklige und stumpfwinklige Dreiecke (vgl. Berechnungsbeispiele).
Zwei deckungsgleiche Dreiecke lassen sich durch Drehen und Verschieben zu einem Parallelogramm zusammensetzen. Deswegen wird eine Dreiecksfläche wie ein halbes Parallelogramm berechnet.
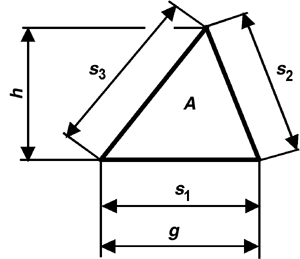
A | Fläche | mm2 | cm2 | dm2 | m2 |
g | Grundlinie | mm | cm | dm | m |
s | Seitenlänge | mm | cm | dm | m |
h | Höhe | mm | cm | dm | m |
l U | Umfang | mm | cm | dm | m |
![]()
![]()
![]()
lU = s1 + s2 + s3
Berechnungsbeispiel 1
Bei der Fertigung eines Werkstücks aus Stahlblechtafeln 2 m x 1 m blieben drei Dreiecke als Verschnitt. Berechnen Sie die Verschnittfläche.
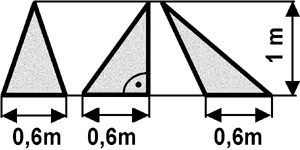
Wertetabelle:
g = 0,6 m
h = 1 m
n = 3
A in m2
Lösung:
![]()
A = 0,9 m2 Verschnittfläche
Erfolgskontrolle: (Überschlag)
(0,6 m2/2) 3 = 0,9 m2
Dreiecke sind bei gleicher Grundlinie und gleicher Höhe flächengleich.
Ergebnis gesichert.
Berechnungsbeispiel 2
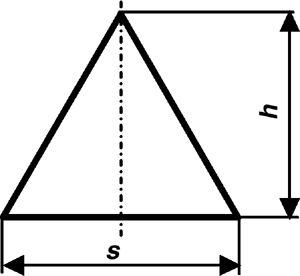
Das Seitenblech einer Maschinenverkleidung ist ein gleichseitiges Dreieck mit 600 mm Seitenlänge. Berechnen Sie Höhe und Fläche des Dreiecks.
Wertetabelle:
s = 6 dm
h in m und A in m2
Lösung:
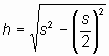
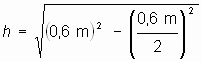
![]()
h = 0,52 m Höhe
![]()
A = 0,156 m2 Fläche
Erfolgskontrolle:
![]()
Ergebnis gesichert.
Berechnungsbeispiel 3
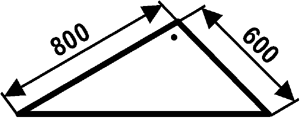
Eine Abdeckung hat die Form eines rechtwinkligen Dreiecks. Berechnen Sie Fläche und Umfang.
Wertetabelle:
a = 0,6 m
b = 0,8 m
A in m2 und lU in m
Lösung:
![]()
![]()
c = 1 m
lU = a + b + c = 0,6 m + 0,8 m + 1 m
lU = 2,4 m Umfang
Erfolgskontrolle:
![]()
(10 dm)2 = (6 dm)2 + (8 dm)2
10 dm + 6 dm + 8 dm = 24 dm
Ergebnis gesichert.
Übungsaufgaben
(1)
Das Seitenblech einer Verkleidung ist ein gleichseitiges Dreieck mit 1 m Seitenlänge. Berechnen Sie Höhe und Fläche des Dreiecks.
(2)
Eine Abdeckung hat die Form eines rechtwinkligen Dreiecks. Berechnen Sie Seitenlänge a, Fläche und Umfang, wenn c = 1,5 m und b = 1,2 m betragen.
© Alle Rechte beim STROBEL VERLAG
