| Ausgabe 5/2005, Seite 8 f. |
Fachmathematik
Einführung in die Fachmathematik
Teil 14: Flächenberechnung Kreis
Die Kreisfläche (A) wird von der Kreislinie (lU), dem Kreisumfang, begrenzt. Der Abstand vom Mittelpunkt (M) eines Kreises zur Kreislinie ist der Radius (r) oder Halbmesser. Die Strecke durch den Mittelpunkt, die in zwei Punkten der Kreislinie endet, ist der Durchmesser (d), dessen Länge 2r ist. Zwischen dem Durchmesser und dem Umfang eines Kreises besteht ein festes Zahlenverhältnis, die Kreiszahl
p = 3,14.![]()
lU = d
p = 2 r p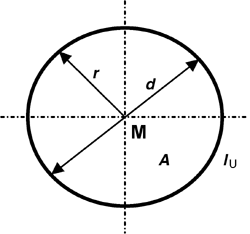
Wird ein Kreis zerteilt (wie eine Torte), so können die Teile zu einem Rechteck gelegt werden.
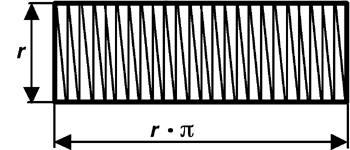
Die Kreisfläche ergibt das Produkt
![]()
![]()
![]()
A | Fläche | mm2 | cm2 | dm2 | m2 |
r | Radius | mm | cm | dm | m |
d | Durchmesser | mm | cm | dm | m |
l U | Umfang | mm | cm | dm | m |
Der Anlagenmechaniker rechnet im Rohrleitungsbau mit dem Durchmesser, bei Blechen und beim Umformen mit dem Radius.
Berechnungsbeispiel 1
Ein Kreis hat 80 cm Durchmesser. Berechnen Sie die Kreisfläche und den Umfang.
Wertetabelle:
d = 0,8 m
A in m2 lU in m
Lösung:
A = d d 0,785
A = 0,8 m 0,8 m 0,785
A = 0,5025 m2 = 0,5 m2 Kreisfläche
lU = d
p = 0,8 m 3,14lU = 2,5 m Kreisumfang
Erfolgskontrolle (Überschlag):
0,5 m2 = 0,8 m 0,8 m 0,8
![]()
Ergebnis gesichert.
Berechnungsbeispiel 2
Ein Kreis hat eine Fläche von 0,8 m2. Wie groß ist sein Durchmesser?
Wertetabelle:
A = 0,8 m2 d in m
Lösung:
![]()
d = 1 m Durchmesser
Erfolgskontrolle:
A = d d 0,785
![]()
Ergebnis gesichert.
Der Kreisausschnitt ist die Fläche, die die Schenkel des Mittelpunktswinkels
a aus dem Kreis schneiden.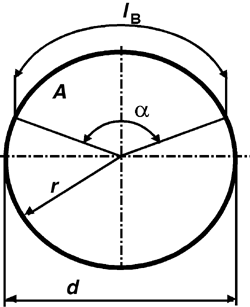
![]()
![]()
Berechnungsbeispiel 3
Ein Kreis hat einen Durchmesser von 1 m. Welche Fläche und welchen Umfang hat ein Kreisausschnitt von 120?
Wertetabelle:
d =1 m a = 120
A in m2 lB in m
Lösung:
![]()
![]()
A = 0,262 m2 Fläche
![]()
![]()
lB = 1,05 m Bogenlänge
Erfolgskontrolle:
![]()
![]()
Ergebnis gesichert.
Kreisabschnitte (Segmente) entstehen, wenn eine Sehne einen Kreis schneidet. Die Fläche eines Kreisabschnitts kann ohne Winkelfunktionen nur angenähert berechnet werden.
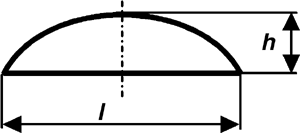
![]()
Übungsaufgaben
(1)
Ein Kreis hat eine Fläche von 1 m2. Berechnen Sie den Durchmesser und den Kreisumfang.
(2)
Ein Kreisausschnitt von 90 hat die Fläche von 0,20 m2. Berechnen Sie den Durchmesser des Kreises.
(3)
Eine gewölbte Abdeckung von 1 m Länge und 0,3 m Höhe hat zwei Seitenbleche in Form eines Kreisabschnitts. Berechnen Sie den Blechbedarf bei 15% Verschnittzuschlag.
© Alle Rechte beim STROBEL VERLAG
