| Ausgabe 3/2005, Seite 6 f. |
Fachmathematik
Einführung in die Fachmathematik
Teil 12: Flächenberechnung Trapez
Ein Viereck, in dem nur zwei gegenüberliegende Seiten parallel sind, heißt Trapez. Zur Berechnung der Fläche wird das Trapez auf das flächengleiche Rechteck mit der Grundseite lm und der Höhe h zurückgeführt. lm ist der Mittelwert, das zahlenmäßige Mittel, der parallelen Seiten l1 und l2.
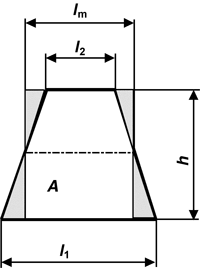
A | Fläche | mm2 | cm2 | dm2 | m2 |
l 1 | untere Länge | mm | cm | dm | m |
l 2 | obere Länge | mm | cm | dm | m |
l m | mittlere Länge | mm | cm | dm | m |
l U | Höhe | mm | cm | dm | m |
A
= lm h![]()
![]()
![]() l1 = 2 lm - l2
l1 = 2 lm - l2
![]() l2 = 2 lm - l1
l2 = 2 lm - l1
![]()
![]()
Berechnungsbeispiel 1
Ein Teilstück einer Dachverkleidung aus Zinkblech hat die Form eines Trapezes. Berechnen Sie (ohne Falzzugabe) den Flächeninhalt.
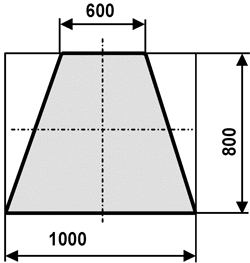
Wertetabelle:
l1 = 1 m l2 = 0,6 m h = 0,8 m
A in m2
Lösung:
![]()
A = 0,64 m2 Werkstückfläche
Erfolgskontrolle:
![]()
![]()
Ergebnis gesichert.
Berechnungsbeispiel 2
Berechnen Sie aus dem Berechnungsbeispiel 1 den Werkstoffverschnitt (AV) in m2 und in Prozent der Werkstückfläche (AW). Bedarfsfläche ist das umschließende Rechteck (AB).
Wertetabelle:
l = 1 m b = 0,8 m AW = 0,64 m2
AB und AV in m2
Lösung:
AB = l b = 1 m 0,8 m = 0,8 m2
AV = AB - AW
AV = 0,8 m2 - 0,64 m2
AV = 0,16 m2 Verschnitt
Erfolgskontrolle:
AV + AW = AB
0,16 m2 + 0,64 m2 = 0,8 m2
Ergebnis gesichert.
Wertetabelle:
g = 0,64 m2 w = 0,16 m2
p in %
Lösung:
![]()
p = 25% Verschnitt
Erfolgskontrolle:
![]()
Ergebnis gesichert.
Berechnungsbeispiel 3
Berechnen Sie aus dem Berechnungsbeispiel 1 die Seitenlänge des Trapezes.
Wertetabelle:
l1 = 1 m l2 = 0,6 m h = 0,8 m
a und s in m
Lösung:
![]()
Die Seitenlänge s errechnet sich in Anlehnung an den Satz des Pythagoras:
![]()
![]()
Die Seitenlänge beträgt 825 mm.
Erfolgskontrolle:
(0,825 m)2 = (0,8 m)2 + (0,2 m)2
Ergebnis gesichert.
Berechnungsbeispiel 4
Ein trapezförmiges Abdeckblech aus Kupfer hat einen Flächeninhalt von 0,8 m2, die parallelen Seiten sind 1 m und 0,6 m lang. Berechnen Sie die Höhe des Blechteils.
Wertetabelle:
A = 0,8 m2 l1 = 1 m l2 = 0,6 m
h in m
Lösung:
![]()
Das Blech ist 1 m hoch.
Erfolgskontrolle:
![]()
A = 0,8 m2
Ergebnis gesichert.
Übungsaufgaben
(1) Für eine Grillhütte ist ein Rauchfang aus nicht rostendem Edelstahlblech nach Skizze anzufertigen. Berechnen Sie den Blechbedarf bei 25% Zuschlag für Verschnitt.
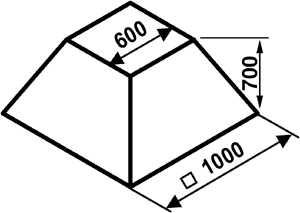
(2) Ein Knotenblech von 4 dm3 Fläche hat Trapezform. Seine Grundlinie misst 30 cm, seine Höhe 20 cm.
Wie lang ist die kürzere der parallelen Seiten ?
© Alle Rechte beim STROBEL VERLAG
