Ausgabe 9/2004, Seite 4 f.

Fachmathematik

Einführung in die Fachmathematik

Teil 6: Dreisatz (1)

In dieser und der nächsten Lektion geht es um die Dreisatzrechnung. An vielen Beispielen wird gezeigt, dass alle Berechnungen nach nur zwei Lösungsansätzen erfolgen: dem direkten und indirekten Verhältnis:

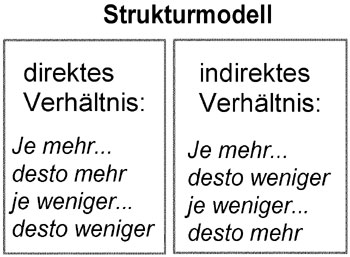
Lösung von Dreisatzaufgaben

Beispielaufgabe

3 Rohre mit gleichem Volumenstrom füllen einen Behälter in 2 Stunden. Welche Zeit benötigen 2 Rohre?

Die Berechnung einer Dreisatzaufgabe beginnt mit dem zweizeiligen "Ansatz". Dies ist eine Gliederung und textliche Verkürzung der Aufgabenstellung. Der Ansatz wird so aufgebaut, dass die gesuchte Größe unten rechts steht:

3 Rohre => 2 Stunden
2 Rohre => x Stunden

Es liegt ein indirektes Verhältnis vor.

Anstelle des Dreisatzes kann die Aufgabe mit einer Gleichung gelöst werden.

Erfolgskontrolle:

3 h · 2 R = 3 R · 2 h

Ergebnis gesichert

Beim so genannten Zweisatzrechnen, entfällt einer der Lösungsschritte, weil er nicht verlangt wird oder in der Aufgabenstellung vorgegeben ist. "Zweisatzrechnen ist verkürztes Dreisatzrechnen."

Aufgabe 1

Eine Gesellenstunde kostet 37,50 Euro.
Wie viele Euro muss ein Kunde für 3,5 Arbeitsstunden bezahlen?

Ansatz:

1 Stunde => 37,50 Euro
3,5 Stunden => x Euro

Es liegt ein direktes Verhältnis vor.

Lösung mit Zweisatz:

1 Stunde => 37,50 Euro
3,5 Stunden => 37,50 Euro · 3,5
3,5 Stunden => 131,25 Euro

Dem Kunden werden 131,25 Euro in Rechnung gestellt.

Lösung mit Gleichung:

Aufgabe 2

Für eine Montagearbeit benötigt ein Geselle 24 Stunden. Wie viele Arbeitsstunden benötigen 4 Gesellen?

Ansatz:

1 Geselle (A) => 24 Stunden (h)
4 Gesellen (A) => x Stunden (h)

Es liegt ein indirektes Verhältnis vor.

Lösung mit Zweisatz:

1 Geselle => 24 Stunden

4 Gesellen => 6 Stunden
4 Gesellen benötigen 6 Stunden.

Lösung mit Gleichung:

Erfolgskontrolle:

6 h · 4 A = 1 A · 24 h

Ergebnis gesichert

Aufgabe 3

Wie lange muss eine Pumpe fördern, wenn 4 (gleiche) Pumpen eine Baugrube in 2 Stunden entleeren?

Ansatz:

4 Pumpen => 2 Stunden
1 Pumpe => x Stunden

Es liegt ein indirektes Verhältnis vor.

Lösung mit Zweisatz:

4 Pumpen => 2 Stunden
1 Pumpe => 4 · 2 Stunden

Eine Pumpe braucht 8 Stunden zur Entleerung der Baugrube.

Lösung mit Gleichung:

Erfolgskontrolle:

1 P · 8 h = 2 P · 4 h

Ergebnis gesichert

Aufgabe 4

Für eine Rolle von 50 m WICU-Rohr 15 x 1 wurden 79,50 Euro bezahlt. Wie hoch war der Preis für 1 m Rohr?

Ansatz:

50 m => 79,50 Euro
1 m => x Euro

Es liegt ein direktes Verhältnis vor.

Lösung mit Zweisatz:

50 m => 79,50 Euro

1 m => 1,59 Euro
Für 1 m Rohr wurden 1,59 Euro gezahlt.

Lösung mit Gleichung:

Erfolgskontrolle:

1,59 Euro / m · 50 m = 79,50 Euro

Ergebnis gesichert

Übungsaufgaben

(1) Bei einer Wassergeschwindigkeit von 1 m/s hat 1 m Kupferrohr 15 x 1 einen Druckverlust von 12,2 hPa. Welchen Druckverlust haben 9 m Rohr unter gleichen Bedingungen?

(2) Um eine Baugrube zu entwässern braucht eine Pumpe 12 Stunden. Wie lange fördern 3 Pumpen unter vergleichbaren Bedingungen?

(3) 200 Verbindungslötungen an Rohren erforderten 3 Stunden und 20 min. Berechnen Sie die durchschnittliche Zeit für eine Lötung.

(4) Eine Lötverbindung mit silberhaltigem Hartlot erfordert eine Arbeitstemperatur von 800°C. Welche Temperatur ist für vier gleiche Rohrverbindungen erforderlich?

Lösung auf Seite 15

Zurück