IKZ-HAUSTECHNIK, Ausgabe 8/1999, Seite 30 ff.
SANITÄRTECHNIK
Warmwasserversorgung
Bestimmung von Speichergröße und Heizleistung zur Bereitstellung von Trinkwarmwasser nach dem Summenlinienverfahren
Kurt Pfeil* · Teil 1
Für den heutigen komfortgewöhnten Menschen ist es eine Selbstverständlichkeit geworden, daß Trinkwasser in ausreichender Menge und zu jeder Zeit zur Verfügung stehen muß. Um die unterschiedlichen Bedarfsfälle abzudecken, benötigt man einen Speicher, der in der Regel über einen Heizkessel aufgeladen wird. Es stellt sich daher die Aufgabe, Wassererwärmungsanlagen mit Wasserbevorratung nach möglichst wirtschaftlichen Gesichtspunkten zu planen. Eine optimale Bemessung solcher Anlagen ist recht schwierig, weil Auslegungsdaten, wie rasch wechselnder Warmwasserbedarf, Speichervolumen, Wärmeerzeugung und Aufheizzeit in ihrer Wechselbeziehung - teilweise mit gegenläufigen Tendenzen - rechnerisch nur ungenau erfaßbar sind. Bei der Auslegung von zentralen Wassererwärmungsanlagen zeigen sich daher große Ermessensspielräume, die dadurch zustande kommen, daß häufig unlogische und hohe Sicherheitszuschläge eingeplant werden. Das Ergebnis sind teure, zu große Anlagen und unwirtschaftlicher Betrieb.
In der Fachliteratur wird das Summenlinienverfahren genannt, ein graphisches Verfahren, mit dem man den Betriebsablauf von Wärmeerzeugung und Warmwasserentnahme im Verlauf einer Betriebsperiode sehr genau darstellen kann. Wärmeerzeugungsanlagen und Speichergröße können optimal aufeinander abgestimmt und dimensioniert werden.
Die Anwendung des Summenliniendiagramms setzt jedoch voraus, daß ein genaues Bedarfsprofil zugrundegelegt werden muß. Dieses läßt sich mit Hilfe von bekannten Tabellen über spezifische Bedarfswerte, von bekannten Spitzendurchflüssen, Gleichzeitigkeitsfaktoren und Tagesbedarfskurven sowie von Messungen, Analysen, Hochrechnungen und Gespräche mit den Anlagenbetreibern ziemlich genau erstellen.
Der Autor dieses Beitrages hat sich eingehend mit der Methode des Summenlinien-Verfahrens befaßt. Ihm ist daran gelegen, die Grundlagen dieser Methode zur Planung von zentralen Trinkwassererwärmungsanlagen mit Speicherbevorratung zu vermitteln. Großer Wert wurde auf die verständliche Erläuterung gelegt. Anschließend werden mehrere Beispielaufgaben mit den zugehörigen Wärmediagrammen aufgezeigt.
Theorie des Summenlinienverfahrens
Die Summenlinie
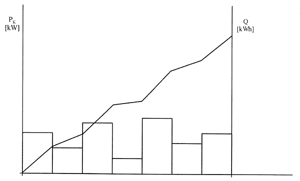
| Bild 1: a) Häufigkeitsverteilung PK = f1(t), b) Summenlinie Q = f2(t) |
Die Verteilung des Warmwasserbedarfs im Verlauf eines Tages kann in einer Verteilungstabelle (ähnlich Tabelle 1 in Teil 3 des Beitrags) dargestellt werden, d.h. für mehrere Verbrauchsabschnitte wird die zugehörige Wasser- oder Wärmemenge aufgelistet. Auch läßt sich diese Verteilungstabelle graphisch in Form einer Häufigkeitsverteilung oder eines Balkendiagramms darstellen (Bild 1). Wenn man auf der Ordinate die Heizleistung PK und auf der Abszisse die Betriebszeit aufträgt, so erhält man die Treppenstufenfunktion PK = f1(t), wobei die Wärmemengen Q durch die Flächeninhalte der Balken beschrieben werden. Jeder einzelne Flächeninhalt wächst linear mit der Zeit, wenn die Leistung des jeweiligen Zeitabschnitts konstant bleibt. Der Flächenzuwachs läßt sich mit der Funktion Q = f2(t) ausdrücken, die sowohl für einen, als auch für die Summe aller Balkenabschnitte Gültigkeit hat. Der Funktionswert f2 (t) gibt den Flächeninhalt aller Balken oder den Gesamtwärmezuwachs von 0 bis t an und stellt somit den Summenlinienverlauf dar. In den folgenden Abschnitten wird die Zuordnung von zwei zueinander korrespondierenden Summenlinien erläutert.
Summenlinien mit gleichen Leistungen für Wärmeerzeugung und Wärmeverbrauch
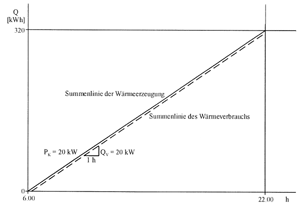
| Bild 2: Summenlinien für Wärmeerzeugung und Wärmeverbrauch (PK = QV) |
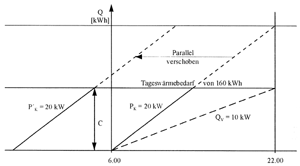
Wenn die Wärmeerzeugung eines Kessels im durchlaufenden Heizungsbetrieb exakt mit dem gleichbleibenden Transmissionswärmebedarf eines Hauses im Verlauf einer Betriebsperiode übereinstimmt, so lassen sich Wärmeerzeugung und Wärmeverbrauch als zwei linear verlaufende übereinanderliegende Summenlinien darstellen (Bild 2). Durch die Steigung der beiden Geraden werden die Leistungen PK und QV beschrieben. Auf dem abgebildeten Diagramm wird beispielsweise eine Leistung von 20 kW mit dem entsprechenden Wärmemengenzuwachs für Erzeugung und Verbrauch in der Zeit von 6.00 Uhr bis 22.00 Uhr dargestellt. Der Betriebsablauf ist gleichzeitig gleichförmig und ununterbrochen.
Summenlinien mit unterschiedlichen Leistungen für Wärmeerzeugung (WE) und Wärmeverbrauch (WV)
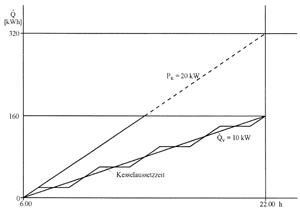
| Bild 3: Summenlinien mit unterschiedlichen Leistungen (PK > |
) Kessel schaltet ein und aus.Sind die Leistungen von WE und WV unterschiedlich, so sind auch die Steigungen beider Geraden unterschiedlich. In Bild 3 ist der WE mit einer Leistung von 20 kW, die des WV’s mit 10 kW Leistung angegeben. Aus Erfahrung wissen wir, daß der Kessel durch Intervallschaltung geregelt wird. Die zu erbringende Wärmemenge wird auf diese Weise der des WV’s angepaßt. Aus Gründen der Anfahr- und Stillstandsverluste muß jedoch die Anzahl der Kesselaussetzzeiten - technisch und wirtschaftlich bedingt - in Grenzen bleiben. Der Betriebsablauf ist gleichzeitig, gleichförmig, der des Kessels ist jedoch unterbrochen.
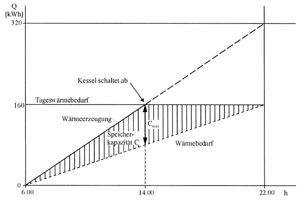
| Bild 4: Summenlinien mit unterschiedlichen Leistungen Kesselanlagen mit Speicher (PK > |
)Das vorgenannte Problem der Anpassung von WE und WV kann auch auf eine andere Weise gelöst werden (Bild 4). Der leistungsmäßig überdimensionierte Kessel liefert im ununterbrochenen Betrieb die für die Betriebsperiode erforderliche Gesamtwärmemenge von 160 kWh. Jedoch muß die Überhangwärme in einem Speicher mit der Speicherkapazität C untergebracht werden. Nach Abschaltung des Kessels wird die erforderliche Bedarfswärme aus dem Speicher entnommen. Diese Lösung stellt technisch eine gute Lösung dar. Unter besonderen Umständen muß aber mit hohen Anlagenkosten und Wärmeverlusten durch Energievorhaltung gerechnet werden. Man kann zu jedem Zeitpunkt den Ladezustand (Kapazität) des Speichers auf der Ordinate ablesen. Gegen 14.00 Uhr ist der Speicher maximal aufgeladen. Nach dieser Kapazität C wird der Speicher ausgelegt. Die Berechnung des Speichervolumens VS aus der vorgegebenen Speicherkapazität C wird im folgenden Beitrag durchgeführt.
Zeitlich verschobene Summenlinien
| Bild 5: Summenlinie der Wärmeerzeugung zeitlich vorverlegt (PK > |
)Wiederum ist die Summenlinie der Wärmeerzeugung mit PK = 20 kW und die Summenlinie des Wärmeverbrauchs mit 
= 10 kW gegeben (Bild 5). Die Heizungsgerade kann durch Parallelverschiebung zeitlich beliebig vorverlegt werden. Die erforderliche Wärme wird teilweise oder vollständig außerhalb der Verbrauchszeit erzeugt. Zur Aufnahme der Wärme ist ein Speicher mit der Kapazität C erforderlich. Auch hierbei ist zu beachten, daß der Kessel nur den Tagesbedarf an Wärme von 160 kWh aufzubringen hat. Der Betriebsablauf ist ungleichförmig, ununterbrochen, nicht gleichzeitig.
Ebenso kann die Heizungsgerade durch Parallelverschiebung zeitlich zurückverlegt werden; d.h. der Kessel beginnt zu einem späteren Zeitpunkt mit dem Heizbetrieb (Bild 6).
| Bild 6: Summenlinie der Wärmeerzeugung zeitlich zurückverlegt (PK > |
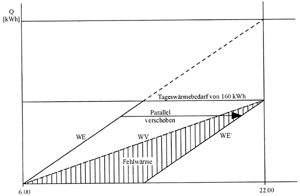
)Aus dem Wärmediagramm erkennt man, daß um 22.00 Uhr die gesamte erforderliche Wärme zur Deckung des Transmissionswärmebedarfs vom Kessel erbracht ist. Dennoch ist die Wärmelieferung unbefriedigend, weil im Verlauf der gesamten Bedarfsperiode und zu jedem Zeitpunkt die Wärmeerzeugung geringer als der Wärmeverbrauch ist. Die Fehlwärme ist als Schraffur dargestellt. Aus dem abgebildeten Diagramm lassen sich zwei wichtige Regeln ableiten:
Regel 1: Am Ende einer Bedarfsperiode muß die gesamt erforderliche Wärmemenge vom Wärmeerzeuger erbracht sein.
Regel 2: Zu jedem Zeitpunkt muß der Wärmebedarf voll gedeckt sein; d.h. die Heizlinie muß an jeder Stelle über dem Wärmeverbrauchsprofil liegen.
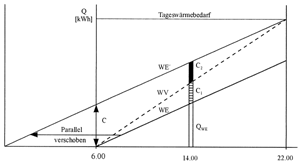
| Bild 7: Summenlinie des Wärmeerzeugers zeitlich vorverlegt ( |
> PK)Das Wärmediagramm von Bild 7 zeigt einen Wärmeverbrauch, der eine erheblich größere Leistung fordert, die ein Wärmeerzeuger mit einer kleineren Leistung bei gleichzeitigem Betriebsablauf nicht aufbringen kann. Man erkennt, daß die Heizlinie durch Parallelverschiebung zeitlich soweit vorverlegt werden muß, bis am Ende der Betriebsperiode (um 22.00 Uhr) volle Wärmedeckung erreicht ist.
Mit der verschobenen Heizlinie des WE’s sind die beiden vorgenannten Regeln erfüllt. Allerdings ist ein Speicher mit der angegebenen Kapazität C erforderlich, der vor dem Beginn des Wärmeverbrauchs aufgeladen wird und seine Wärme ergänzend zu der Wärmelieferung des Kessels kontinuierlich abgibt. Man kann unschwer ablesen, wieviel Wärme Kessel QWE und Speicher C1 in der Zeit von 6.00 Uhr bis 14.00 Uhr geliefert haben. C2 stellt die Restwärme im Speicher dar, die um 22.00 Uhr aufgebraucht ist.
WE- und WV-Profile für Duschen und Baden
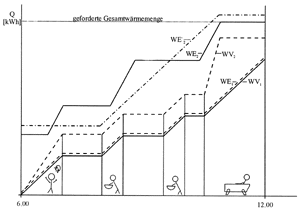
| Bild 8: Wärmeverbrauchs- und Wärmeerzeugungsprofile für Dusche und Wanne. |
Die Warmwasserversorgung eines Duschbades, eines Wannenbades und zweier Waschtischbenutzungen ist in Bild 8 dargestellt. Für die Warmwasserbereitung WE steht ein Durchflußwassererwärmer mit einer Leistung von 18 kW zur Verfügung. Das Wasser kann nur eine begrenzte Wärmemenge WV1 aufnehmen. Wärmeverbrauchs- und Wärmeerzeugungsprofile liegen aufeinander. Diese Art der Warmwasserversorgung ist unbefriedigend, weil für die Dusche eventuell eine größere Wasserspende und für die Wanne eine schnellere Auffüllzeit erwartet wird. Man muß daher von einem Verbrauchsprofil WV2’ ausgehen, welches eine Kesselanlage mit Speicher erfordert. Damit die beiden vorgenannten Regeln erfüllt sind, muß über dem Verbrauchsprofil WV2 eine Kessellinie WE2 oder WE2’ (vorerst willkürlich) gezeichnet werden. Die genaue Untersuchung über Kesselleistung, Anzahl der Betriebsunterbrechungen und Speicherkapazität erfolgt im zweiten Teil. (Fortsetzung folgt)
Formelzeichen und Einheiten
Formelzeichen | Einheit | Bedeutung des Formelzeichens |
Q | [kWh] | Wärme |
QK | [kWh] | Wärmeerzeugung |
QV | [kWh] | Wärmeverbrauch |
QWE | [kWh] | Wärmeerzeugung eines WE |
| [kW] | Leistung |
| [kW] | Leistungsaufnahme eines WV |
PK | [kW] | Kesselleistung |
C | [kWh] | Wärmeinhalt des Speichers |
c | [kJ/(kg · K)] | Spez. Wärmekapazität |
| [°C] | Speichertemperatur |
| [°C] | Kaltwassertemperatur |
| [K] | Temperaturdifferenz |
| [kg/m3] | Dichte |
tB | [h] | Betriebszeit in Stunden |
h | [-] | Uhrzeit |
| [-] | Wirkungsgrad |
| [-] | Nutzungsgrad = 1/ |
| [-] | Ausnutzungsfaktor = 1/ |
VS | [m3] | Speichergesamtvolumen |
VN | [m3] | nutzbares Speichervolumen |
WE | [-] | Wärmeerzeuger |
WV | [-] | Wärmeverbraucher |
*) Prof. Dipl.-Ing. Kurt Pfeil, Fachhochschule Köln, Fachbereich Versorgungstechnik, Dozent für Sanitärtechnik
L i t e r a t u r :
[1] Bösch, K.: SI-Berechnungsgrundlagen
[2] Sander, H.: Warmwasserbereitungsanlagen für Wohn- und Zweckgebäude, Gewerbe und Industrie; 2. Auflage 1963, Haenchen und Jäh, Berlin.
[3] Stiebel Eltron: Warmwasserspeicher
[4] Dipl.-Ing. Dirk Wagner: Diagramme
[Zurück] [Übersicht] [www.ikz.de]