Einführung in die Elektronik

Wechselstromwiderstände - Bauelemente der Elektronik

Ing. Günter E. Wegner Teil 6

Der Wirkwiderstand, wie er in der letzten Folge besprochen wurde, übt seine strombremsende Wirkung in einem Gleichstrom- genauso wie in einem Wechselstromkreis aus. Es gibt aber Widerstände, die bei Wechselstrom ein anderes Verhalten zeigen als bei Gleichstrom. Bauteile mit einem solchen Verhalten heißen "Wechselstromwiderstände oder - mit Fremdwort - "Impedanzen" und gemeint sind Kondensator und Spule, zwei ebenfalls wichtige Bauelemente der Elektronik. In dieser Folge soll zunächst der Kondensator besprochen werden.

Aufbau des Kondensators

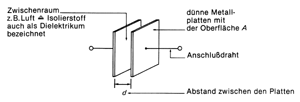
Kondensatoren ähneln äußerlich dem Widerstand. Sie sind aber völlig anders konstruiert und erfüllen in einer elektronischen Schaltung völlig andere Aufgaben. Die grundsätzliche Eigenschaft des Kondensators ist die Fähigkeit, elektrische Energie zu speichern. In der Grundform besteht ein Kondensator aus zwei sich parallel gegenüberstehenden Metallplatten. Beide Platten sind zunächst elektrisch neutral, d.h. auf keiner besteht ein Mangel oder ein Überschuß an Elektronen. Das Bild ändert sich aber, wenn man an die Platten eine Gleichspannung anlegt. Der Ladungszustand der Spannungsquelle - Elektronenüberschuß an dem einen, Elektronenmangel an dem anderen Pol - teilt sich den beiden metallenen Platten oder Belägen mit. Das bedeutet: von einem Belag werden Elektronen abgesaugt, dem anderen werden Elektronen zugeführt. In den Zuleitungen und auf den Platten findet also ein Elektronentransport statt, was bedeutet, daß ein elektrischer Strom fließt (obwohl kein geschlossener Stromkreis vorhanden ist, denn die Luft zwischen den Platten wirkt wie ein Isolator). Der Strom fließt dann auch nur so lange, bis der Elektronenaustausch bzw. -Ausgleich vollzogen ist, die Elektronen entsprechend "verschoben" wurden. Verständlich ist, daß dieser "Verschiebestrom" um so größer wird, je mehr Elektronen sich ausgleichen müssen, d.h. je höher die anliegende Spannung und je größer die Oberfläche der Platten ist. Aber auch, je geringer der Abstand der beiden Platten oder Beläge voneinander ist. Um so besser kann dann die Spannung auf die Elektronen einwirken. Man bezeichnet diesen Vorgang als "Laden des Kondensators" und den auftretenden Verschiebestrom als "Ladestrom". Ist der Ladevorgang abgeschlossen, fließt kein Strom mehr, obwohl die Spannung weiter anliegt. Wird die Spannungsquelle - eine Batterie etwa - entfernt, ändert sich der Ladungszustand der Platten nicht - der Kondensator bleibt aufgeladen. Man kann die Ladung wieder zum Verschwinden bringen, den Kondensator "entladen" wenn man die beiden Beläge z.B. über einen Widerstand, miteinander verbindet. Durch den Widerstand fließt dann so lange ein Elektronenstrom von der negativen zur positiven Platte, bis der Ladungsunterschied ausgeglichen ist.

Bild 1: Grundaufbau eines Kondensators. (HEA)

Die Kapazität des Kondensators

Die Kenngröße des Kondensators ist sein Speicher- oder Fassungsvermögen für die elektrische Ladung. Es wird "Kapazität" des Kondensators genannt, mit dem Formelzeichen C. Die Maßeinheit der Kapazität ist das Farad F und wie folgt definiert: Ein Kondensator hat die Kapazität von 1 F, wenn in ihm bei einer angelegten Spannung von 1 Volt eine Sekunde lang ein Strom von 1 Ampere fließt. Als Formel geschrieben:

Für die Praxis ist das Farad erheblich zu groß, es wird daher wie folgt unterteilt:

1 Millifarad = 1 mF = 10^-3 F

1 Mikrofarad = 1 湩 = 10^-6 F

1 Nanofarad = 1 nF = 10^-9 F

1 Picofarad = 1 pF = 10^-12 F

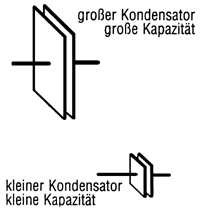
Die Kapazität des Kondensators wird bestimmt von der Größe der Platten oder Beläge, ihrem Abstand und dem Material zwischen den Platten, dem sog. Dielektrikum.

Bild 2: Die Kapazität des Kondensators wird auch von der Plattengröße bestimmt.

Ladung des Kondensators

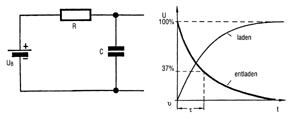
Wird ein Kondensator mit der Kapazität C über einen vorgeschalteten Widerstand R an eine Batterie mit der Spannung U angeschlossen, so fließt im Augenblick des Einschaltens der höchste Ladestrom, weil der Kondensator ja noch völlig "leer" ist. Der Ladestrom wird nur durch den Widerstand R begrenzt - ohne R würde der Kondensator für die Batterie wie ein Kurzschluß wirken. Dann jedoch wird sich der Ladestrom stetig verringern, weil die auf den Belägen sich ansammelnden Elektronen eine Gegenspannung aufbauen und den Ladestrom bremsen. Schließlich wird diese Gegenspannung, die Spannung über den Kondensatorplatten, ebenso groß wie die anliegende Batteriespannung U. Der Ladevorgang ist beendet, es fließt kein Strom mehr. Ladestrom und Ladespannung haben demnach einen gerade umgekehrten Verlauf, was man in einer Grafik sehr schön darstellen kann - Bild (3) man sieht, daß die Änderungen von Strom und Spannung zuerst schnell erfolgen, die Kurven dann aber in einem flacheren Verlauf übergehen.

Bild 3: Schaltung und Kurvenverlauf der Kondensatorauf- und Entladung. Mit angedeutet in der Kurve ist die Zeitkonstante. (HEA)

Entladung des Kondensators

Für den Vorgang der Entladung des Kondensators verlaufen die Kurven für Strom und Spannung spiegelbildlich. Es fließt ein Entladestrom, der stetig abnimmt, zunächst schnell, dann verlangsamt. Für die Lade- bzw. Entladezeit eines Kondensators gibt es in der Elektronik einen oft verwendeten Begriff, der dem Fachmann Information über Ladezeit und Ladezustand des Kondensators vermittelt. Gemeint ist die sog. Zeitkonstante, die hier kurz angeschnitten werden soll. Die Zeitkonstante ergibt sich aus der Festlegung, daß ein Kondensator auf 63% der angelegten Spannung aufgeladen bzw. auf 37% entladen ist, wenn eine bestimmte Zeit, eben die Zeitkonstante, vergangen ist. Die Zeitkonstante erhält man aus dem Produkt Kapazität mal Ladewiderstand und praktisch gilt ein Kondensator als völlig geladen bzw. entladen nach einer Zeit, die fünfmal so lang ist wie eine Zeitkonstante, also nach dem Ablauf von fünf Zeitkonstanten. Die Zeitkonstante hat in elektronischen Schaltungen, vor allem bei deren Entwicklung, eine große Bedeutung.

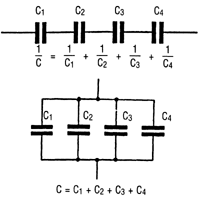
Bild 4: Reihen- und Parallelschaltung von Kondensatoren.

Der Kondensator an Wechselspannung

Der Kondensator ist, wie das Vorgesagte zeigt, für Gleichstrom undurchlässig. Er stellt theoretisch einen unendlich großen Widerstand dar, denn nach abgeschlossener Ladung fließt kein Strom mehr. Anders aber, wenn eine Wechselspannung an den Kondensator gelegt wird. Die Wechselspannung ändert, wie man weiß, fortwährend ihre Polarität und diesen Polaritätswechsel müssen zwangsläufig die angeschlossenen Kondensatorbeläge mitmachen. Die Elektronen werden im Takte der Wechselspannung hin und her "gejagt" - es fließt ein ständiger (Wechsel)Strom. Es ist leicht einzusehen, daß die Höhe dieses Stromes von der Frequenz der Wechselspannung abhängt. Je höher die Frequenz der Wechselspannung, um so öfter werden die Elektronen in der Zeiteinheit hin und her gejagt aber auch je größer die Kapazität ist, um so mehr Elektronen müssen transportiert werden. Dabei ist festzuhalten, daß dieser Strom nur in den Zuleitungen des Kondensators fließt, nicht über die zwischen den Platten vorhandene Isolierung. Praktisch wirkt es sich so aus, als ob der Kondensator den Wechselstrom hindurchläßt - ein eingeschaltetes Amperemeter würde den Stromfluß anzeigen. Der Kondensator stellt damit für Wechselstrom einen Widerstand dar, den man als "kapazitiven Widerstand" oder als Blindwiderstand X_c bezeichnet. Auch vom "Wechselstromwiderstand" wird gesprochen, da dieser Widerstand nur bei Wechselstrom in Erscheinung tritt. Errechnen kann man den Blind- oder Wechselstromwiderstand nach der Formel

worin (v) die sog. Kreisfrequenz 2 p f = 6,28 f ist. Die Formel bestätigt, daß der kapazitive Widerstand X_c zunimmt, wenn die Frequenz niedriger und die Kapazität des Kondensators größer wird.

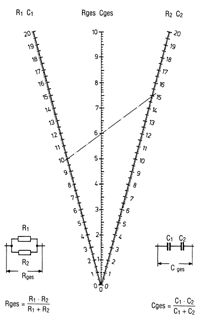
Bild 5: Mit diesem Nomogramm lassen sich Ohmsche Widerstände in Parallelschaltungen und Kapazitäten in Reihenschaltungen einfach berechnen.

Schaltung der Kondensatoren

Kondensatoren kann man, ähnlich wie Wirkwiderstände, in Reihe oder parallel schalten. Dabei verändert sich der resultierende Wert der Kapazität, also das Fassungsvermögen der Schaltung. Sicher nicht schwer zu verstehen, daß bei der Parallelschaltung mehrerer Kondensatoren sich die Gesamtkapazität erhöht. Die Parallelschaltung wirkt so, als ob die Oberfläche der Platten vergrößert wird. Somit kann man rechnen:

C_ges = C₁ + C₂ + C₃ .... (9)

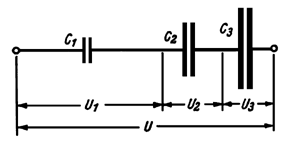
Bei der Parallelschaltung liegen alle Kondensatoren an der gleichen Spannung und die Ladeströme teilen sich im Verhältnis der Kapazitäten auf. Schaltet man die Kondensatoren in Reihe, ist die Wirkung so, als ob der Plattenabstand vergrößert würde; die Gesamtkapazität wird geringer, sie wird kleiner als die Kapazität des kleinsten Kondensators der Reihenschaltung. Jetzt muß man rechnen:

In der Praxis liegen selten mehr als zwei Kondensatoren in Reihe und man kann mit einer vereinfachten Formel arbeiten:

Wer nicht gerne rechnet, benutzt das Nomogramm Bild 5 und ermittelt die Reihenschaltung von Kondensatoren oder die Parallelschaltung von Widerständen grafisch. Etwas mehr Überlegung bedarf es, um die Aufteilung der Spannung zu untersuchen. Auch bei der Reihenschaltung von zwei oder mehr Kondensatoren muß die Anzahl der Elektronen, die auf den ersten Kondensator strömen, genau so groß sein wie die Anzahl der Elektronen, die vom letzten Kondensator abfließen. Daraus folgt, daß die Zahl der Elektronen, besser ausgedrückt, die Ladungsgröße, auf jedem Kondensator gleich groß sein muß. Diese Ladungsmenge Q erhält man nach der Formel:

Q = U C (12)

Damit Q auf jedem Kondensator gleich groß ist, muß das Produkt aus Spannung U und Kapazität C auf jedem Kondensator gleich groß sein. Daraus folgt: ist die Kapazität C klein, ist die Spannung U groß und umgekehrt. Für die Reihenschaltung von Kondensatoren gilt also, daß am Kondensator mit der kleinsten Kapazität die größte Spannung liegt - die Spannungen sich umgekehrt verhalten wie die Kapazitäten. Die Nichtbeachtung dieser Tatsache hat schon so manchen Kondensator das "Leben" gekostet.

Bild 6: Bei der Reihenschaltung von Kondensatoren ist die Spannungsaufteilung zu beachten.

Bauformen des Kondensators

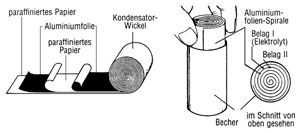
Der Einsatzbereich von Kondensatoren in Elektrotechnik und Elektronik ist vielfältig. Kondensatoren riegeln Gleichspannungen ab und übertragen gleichzeitig Wechselspannungen. So etwa in elektronischen Schaltungen, um zwei Verstärker- oder Schaltstufen miteinander zu verbinden. Kondensatoren verbinden Schaltungspunkte, die keine Signal- oder Impulsspannungen führen dürfen, mit dem Bezugpotential, z.B. in Funkenstörschaltungen. Entsprechend der Anwendungsvielfalt ist die Palette der Kapazitäten und der Bauformen. Kondensatoren mit einem bestimmten Kapazitätswert, also Festkondensatoren, gibt es bis zu etwa 1 湩 und sie sind als sog. Wickelkondensatoren aufgebaut. Die beiden Beläge werden aus Streifen dünner Metallfolie gebildet, zwischen denen als Isolation oder Dielektrikum paraffiniertes Papier oder Kunststoffolie liegt. Das Ganze wird zu einem Wickel aufgerollt und mit Kunststoff vergossen. Eine andere Bauform sind die scheiben- oder röhrchenförmigen Keramikkondensatoren. Sie haben sehr gute elektrische Eigenschaften, besonders im Hochfrequenzbereich. Hohe Kapazitätswerte, bis zu etwa 10.000 湩, werden als "Elektrolyt-Kondensatoren" (Kurzform "Elko") gebaut. Dazu werden Alu-Beläge in eine elektrisch leitende Flüssigkeit, eben den Elektrolyten, eingebracht. Dadurch überzieht sich das Aluminium mit einer hauchdünnen, isolierenden Oxydschicht, die das Dielektrikum bildet und den Abstand der beiden Beläge auf ein Minimum reduziert. Rauht man zudem die Alufläche auf, vergrößert sich die wirksame Oberfläche und man erhält hohe Kapazitätswerte auf engstem Raum. Auch bei Kondensatoren sind die Kapazitäts- und Toleranzwerte in Normreihen gegliedert. Sie sind mit denen der Widerstände vergleichbar und werden bei kleinen Kondensatoren in den gleichen Farbcode angegeben - siehe Bild 5 in Teil 4. Neben der Kapazität spielt die Spannungsfestigkeit des Kondensators eine wichtige Rolle. Sie ist auf dem Kondensator aufgedruckt und ist die Spannung, die der Kondensator maximal im Betrieb vertragen kann. Dabei ist zu beachten, daß neben der Gleichspannung oft noch eine Wechselspannung am Kondensator liegt. Der Maximalwert der Wechselspannung muß dann der Gleichspannung hinzuaddiert werden.

Bild 7: Konstruktion des Elektrolytkondensators.

[Zurück] [Übersicht] [www.ikz.de]