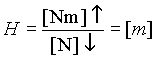IKZ-HAUSTECHNIK, Ausgabe 10/1996, Seite 26 ff.
HEIZUNG/SANITÄR
Formelzeichen und Maßeinheiten in der Pumpentechnik
Dipl.-Ing. Klaus Walter
Der Sinn und der Zweck einer jeden Pumpe besteht darin, eine bestimmte Menge einer Flüssigkeit in einer bestimmten Zeit zu einem bestimmten Ort zu bringen. Neben einer Vielzahl von Berechnungswerten, die man in der Pumpentechnik kennt, sollen nachfolgend schwerpunktmäßig der Förderstrom und die Förderhöhe einer Pumpe behandelt werden.
1. Einleitung
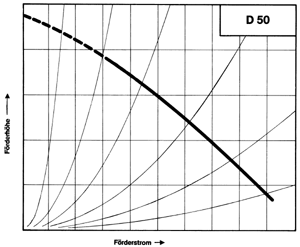
Bild 1 zeigt die allgemein bekannte Darstellung einer Pumpenkennlinie. In diesem Diagramm werden diese beiden Förderkriterien und die Art ihrer Abhängigkeit voneinander graphisch dargestellt.
Die Auslegung des Förderstroms richtet sich nach dem Bedarf am Verbrauchsort. Das ist im Falle einer Heizung der Wärmebedarf des zu beheizenden Gebäudes. Er wird nach der Norm DIN 4701 und weiterer Verfahren bestimmt. Im Falle einer Druckerhöhungsanlage ist die Norm DIN 1988 Grundlage für die Lieferung zu den Entnahmestellen.
| Bild 1: Pumpenkennlinie; Förderstrom und Förderhöhe stehen in einer Abhängigkeit zueinander. |
Das durch die Rohrleitungen strömende Wasser bewirkt einen Rohrreibungswiderstand, der von der Pumpe überwunden werden muß. Er ist ein elementarer Bestandteil zur Auslegung der notwendigen Förderhöhe. Bedauerlicherweise gibt es für diese Berechnungsgänge keine DIN-Norm als Grundlage.
Der Berechnung einer dieser Förderleistungen liegt eine physikalische Formel zugrunde. Das Ergebnis wird in seiner Größe mit einer Maßeinheit versehen.
Selbst unter Fachleuten werden diese kurz definierten Begriffe häufig verwechselt oder teilweise auch nur unkorrekt benutzt. In gewissen Grenzfällen entzündet sich daran sogar eine heftige Diskussion. Die nachfolgende Abhandlung ist der Versuch, Klarheiten zu schaffen. Da das aber nicht immer möglich ist, werden die verschiedenen Einsatz- und Gebrauchsmöglichkeiten aufgezeigt.
1.1 Darstellung physikalischer Größen
Eine physikalische Größe kann exakt nur durch zwei Angaben, eine quantitative und eine qualitative, dargestellt werden [1]:
Die quantitative Angabe kennzeichnet den Zahlenwert oder die Anzahl der Einheiten. Die qualitative Angabe gibt Auskunft über die Art der Größe, über ihre Dimension oder Maßeinheit. Wird mit (G) der Zahlenwert irgendeiner physikalischen Größe G und mit [G] die Einheit der Größe G bezeichnet, so kann diese durch die folgende Gleichung dargestellt werden:
G = (G) · [G]
z.B.: l = (3,5) · [m]
oder: 
= (7,8) · [l/s]
Auf die Anwendung wird später eingegangen.
1.2 Gesetzliche Einheiten im Meßwesen
Schon im Jahre 1876 verständigten sich einige Länder, dazu zählte auch das Deutsche Kaiserreich, auf die Verwendung einheitlicher Maßeinheiten nach dem metrischen, d.h. einem dezimal teilbaren System. Als wichtigstes wurde mit dem Meter als Längenmaß und dem Kilogramm als Gewicht begonnen.
Daraus entwickelte sich das Internationale System der Maßeinheiten, das SI-System (französisch: Système International d’Unités). Für die Bundesrepublik Deutschland ist dieses SI-System als "Gesetz über Einheiten im Meßwesen" durch den Deutschen Bundestag beschlossen und am 2. Juli 1969 verkündet worden. Nach einer Einführungs- und Übergangszeit wurde es am 1. Januar 1978 allein verbindliche Grundlage aller Arten von Messungen.
Sämtliche davor bestehenden Maßsysteme sind nicht nur ungültig. Ihre Anwendung ist verboten.
Das Deutsche Institut für das Normenwesen DIN hat sämtliche maßeinheitlichen Begriffe als DIN 1301 "Einheiten, Einheitennamen, Einheitenzeichen" [2] festgeschrieben.
| Bild 2: Die Maßeinheiten im SI-System; aus nur 3 Basiseinheiten entwickeln sich die für die Pumpentechnik erforderlichen Maßeinheiten. (Bild: Autor) |
Als Basiseinheiten sind 7 Begriffe definiert. Sie sind im Bild 2, oben, aufgeführt. Für die hier behandelten Themen aus der Pumpentechnik sind aber nur die ersten drei Einheiten (kg, m, s) von Interesse. Durch einfachste physikalische Verknüpfungen entwickeln sich daraus sogenannte abgeleitete Einheiten. Ab einer bestimmten Größe verlieren diese aber an Übersichtlichkeit. Es werden neue Einheitennamen (z.B. Newton, Joule, Pascal) festgelegt.
2. Der Förderstrom
In einem Pumpenkennliniendiagramm wird der Förderstrom auf der waagerechten Achse, der Abszisse, dargestellt. Die ersten Schwierigkeiten kommen auf, wenn man diese Achse beschriften soll.
2.1 Benennung der Achse
Für "Kreiselpumpen und Kreiselpumpenanlagen" gilt die Norm DIN 24260, Teil 1 [3]. Darin wird der von der Pumpe durch ihren Austrittsquerschnitt geförderte Volumenstrom als "Förderstrom" definiert. In zusammengesetzten Begriffen findet sich auch das Wort "Volumenstrom". Wenn die Dichte des Mediums berücksichtigt werden muß, wird vom "Massestrom" gesprochen.
Zur "Ermittlung der Rohrdurchmesser" für Trinkwasser-Installationen gilt die Norm DIN 1988, Teil 3 [4]. Darin wird der gleiche Begriff als "Volumenstrom" definiert. Es tritt, speziell im Zusammenhang mit den Armaturenberechnungen, auch der Begriff "Durchfluß" auf.
Diese Unterschiede sind im Bild 3 aufgeführt.
Bild 3: Definitionsunterschiede in verschiedenen Normen für Förderstrom und Förderhöhe.
Kreiselpumpenanlagen | ||
Benennung | Formelzeichen | Einheit |
Förderstrom, |
| m3/h, l/s |
Förderhöhe | H | m |
Druckerhöhungsanlagen | ||
Benennung | Formelzeichen | Einheit |
Durchfluß, |
| m3/h, l/s |
Förderdruck, | Dpp | bar, mbar, Pa |
·2.2 Formelzeichen der Achse
In der Norm DIN 24260 wird durchgehend das physikalische Formelzeichen Q für die geförderten Ströme benutzt. Die deutschen Pumpenhersteller verwenden deshalb fast ausschließlich dieses Zeichen in ihren Katalogen. Für einen Massestrom findet das Formelzeichen q Verwendung. Daneben läßt diese Norm (in Klammern) auch die Formelzeichen und qv für den Förderstrom sowie die Zeichen 
und qm für den Massestrom zu.
Ganz anders und eindeutig ist die Festlegung in der DIN1988. Das einzig zugelassene Zeichen ist für den Volumenstrom. Auch diese Unterschiede sind im Bild 3 dargestellt.
2.2.1 Fazit
Welche Einheit sollte zweckmäßigerweise allgemein angewendet werden? Während die eine deutsche Norm einen breiten Spielraum läßt, definiert die andere eindeutig. Eine einfache Betrachtung führt zur Bezeichnung für ein in einem Zeitabschnitt transportiertes Volumen.
Denn: Bei Pumpenkennlinien in der Heizungstechnik ist das Formelzeichen zulässig. Bei Pumpenkennlinien in der Sanitärtechnik ist das Formelzeichen Q dagegen nicht zulässig.
Außerdem ist Q für eine in einer Zeit bewegte Fördermenge falsch. Mit "Q" bezeichnet man in der Physik zunächst ganz allgemein eine existierende Menge (eines Stoffes, einer Energie oder einer anderen Erscheinungsform). Will man eine Zeitabhängigkeit darstellen, ist ein Punkt über dem Formelzeichen für die erste Ableitung dq/dt erforderlich. Würde man aber den Förderstrom einer Flüssigkeit mit 
bezeichnen, käme man in der Heizungstechnik in arge Bedrängnis mit dem ebenso definierten zeitabhängigen Wärmebedarf eines Gebäudes in W bzw. kW.
2.3 Einheiten der Achse
Hier gibt es keine Komplikationen. Es finden abgeleitete SI-Einheiten des Volumens (l, m3), dividiert durch die Zeit (s, min, h) Anwendung.
Der in der DDR häufiger als in der Alt-BRD verwendete Begriff des Massestroms in kg/h wurde (wie einiges andere) ein Opfer der Wiedervereinigung.
3. Die Förderhöhe
In einem Pumpenkennliniendiagramm wird die Förderhöhe auf der senkrechten Achse, der Ordinate, dargestellt. Unter diesem Begriff "Förderhöhe" ist aber nicht ein realer Wassertransport auf diese so definierte Höhe gemeint.
Zum besseren Verständnis diene die nachfolgend beschriebene Versuchsanordnung: Man stelle sich eine Pumpe mit senkrechtem Druckstutzen vor. Darauf ist ein senkrechtes, oben offenes Glasrohr in unbestimmter Länge befestigt. Wenn die Pumpe betrieben wird, ist sie in der Lage, das Wasser in diesem Steigerohr auf eine bestimmte Höhe zu drücken. Die Ansaugung erfolgt aus einem offenen Behälter, um den Luftdruckeinfluß zu eliminieren.
Um das Wasser in dieser geförderten Höhe zu halten, ist der Fortbetrieb der Pumpe erforderlich. In dieser Situation hat das Wasser keine Bewegung mehr, also auch keine Rohrreibungs- oder sonstigen Verluste.
Das Maß dieser Betriebs-Wassersäule ist ein Längenmaß (in m). Es hat aber keinen realen Nutzen. In der Praxis ist es nötig, die Förderhöhe der Pumpe nach ihrer Betriebsart im Rohrleitungssystem zu bestimmen.
Bei Druckerhöhungsanlagen setzt sich die notwendige Förderhöhe HDEA der Pumpe zusammen aus
- der geodätischen Höhe Hgeo, auf die das Wasser zu heben ist,
- der Verlusthöhe HVerl, die durch die Rohrleitungswiderstände bestimmt wird,
- dem gewünschten Restfließdruck HRF an der höchsten Entnahmestelle, um in der obersten Hoteletage noch behaglich duschen zu können.
HDEA = Hgeo + HVerl + HRF (in m)
Bei Heizungsanlagen hat die Pumpe lediglich die Aufgabe, die im Rohrkreislauf auftretenden Verluste zu überwinden. Die Gebäudehöhe spielt dabei nicht die geringste Rolle.
HHzg = HVerl (in m)
3.1 Benennung der Achse
Für "Kreiselpumpen und Kreiselpumpenanlagen" definiert die Norm DIN 24260 Teil 1 [3] die Förderhöhe der Pumpe. Weiter werden in den einzelnen Abschnitten spezifiziert:
Geodätische Höhe, Druckhöhe, Geschwindigkeitshöhe, Energiehöhe, Verlusthöhe und NPSH-Höhe.
Ganz anders ist die Norm DIN 1988 Teil 5 [4] angelegt. Sie beschäftigt sich mit den Begriffen Druckerhöhung und Druckminderung. Der von der Druckerhöhungsanlage (DEA) zu erbringende Förderdruck wird als Differenzdruck DpP zwischen den Druckzuständen nach und vor der DEA betrachtet.
DpP =pnach - pvor
Diese Unterschiede sind ebenfalls im Bild 3 aufgeführt.
Das technische Gerät, welches diese Druckerhöhung aufbauen soll, also die Pumpe, wird in dieser Norm überhaupt nicht näher beschrieben.
3.2 Einheiten der Achse
An der Frage, welche Maßeinheit die senkrechte Achse der Pumpenkennlinie haben muß, entzünden sich die meisten kontroversen Diskussionen.
An Pumpenkennlinien (Bild 1) wird die Förderhöhe üblicherweise in Metern (m) angegeben.
Die Förderhöhe einer Pumpe ist jedoch nichts anderes als die Erzeugung einer Druckdifferenz. Bei einer DEA ist es die Erhöhung eines zur Verfügung stehenden Vordrucks. Bei Heizungsanlagen ist es die Addition auf den im System herrschenden Ruhedruck. Damit böte es sich an, für die Förderhöhe die SI-Druck-Einheit Pascal (Pa) zu verwenden.
Es ist die Frage aufzuwerfen, ob man ein und dieselbe physikalische Funktion in m und in Pa umschreiben kann. Das soll untersucht werden. Die physikalische Formel für die Förderhöhe lautet:
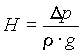
Mit Dp in Pa = N/m2 oder entsprechend Bild 2: Dp in kg/(m · s2), mit r in kg/m3 und mit g in m/s2 ergibt sich in der Einheitendarstellung:
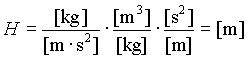
Wenn man eine Rohrnetzberechnung durchführt, so werden mehrere Rohrstücke mit ihren verbrauchten Druckdifferenzen addiert. Es wäre ein zu großer Aufwand, die beiden Naturkonstanten 
und g in jedem Summanden zu berücksichtigen. Sie werden deshalb mathematisch ausgeklammert:
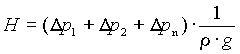
Die Klammer hat nun eindeutig die für Druckdifferenzen richtige Maßeinheit Pa. Damit ist der Norm DIN 1988 Genüge getan. Damit ist aber nicht die technische Funktion der Pumpe beschrieben, die diese Druckdifferenz zu überwinden hat.
Die Förderhöhe der Pumpe ist in der DIN 24260 Teil 1 [3] beschrieben als die von der Pumpe auf die Förderflüssigkeit übertragene nutzbare mechanische Arbeit (in Nm, nach oben wirkend), bezogen auf die Gewichtskraft (in N, nach unten wirkend). Als Einheitengleichung stellt sich das so dar:
3.2.1 Fazit
Im Kennliniendiagramm einer Pumpe ist die Maßeinheit m für die Förderhöhe richtig. Das wurde im vorausgegangenen Abschnitt verdeutlicht. Davon wird überhaupt nicht berührt, daß Rohrnetzberechnungen in Pa durchgeführt werden. Wichtig ist es nur, die richtige Umrechnung bei der Pumpenauswahl durchzuführen. Dazu soll die Gegenüberstellung im Bild 4 helfen.
Bild 4: Gegenüberstellung verschiedener Maßeinheiten für Drücke und Förderhöhen. (Bild: Autor)
bar | Pa | m |
1 | 100000 | 10 |
0,1 | 10000 | 1 |
0,01 | 1000 = 1 kPa | 0,1 |
0,001 = 1 mbar | 100 = 1 hPa | 0,01 = 1 cm |
0,0001 | 10 | 0,001 |
0,00001 | 1 | 0,0001 |
Die Maßeinheit Pascal ist zunächst für den Praktiker etwas "unhandlich". Deshalb verwendet man häufig dezimale Vielfache, um verständliche Zahlenwerte zu erhalten. Im Bild 4 wird deutlich, daß sich die Einheit hPa besonders gut für vergleichende Betrachtungen eignet. Denn 1 hPa ist 1 mbar.
Auch für Messungen von Druckdifferenzen mit einem U-Rohr-Manometer ist diese Einheitengröße praktisch. Denn 1 hPa entspricht 1 cm Differenz in den Wasserschenkeln.
3.2.2 Die "Wassersäule"
Eine kurze Betrachtung noch zu der nicht ausrottbaren, veralteten Maßeinheit "Meter Wassersäule / mWS". Sie ist durch das SI-System und das Einheitengesetz abgeschafft worden. Die alleinige Messung in Meter/m ist zutreffend und ausreichend.
Außerdem dürfte aus den Ausführungen - gepaart mit der einleitenden Versuchsbeschreibung - klar sein, daß eine Pumpe in einem Rohrsystem alles andere drückt, nur keine in Metern meßbare Wassersäule.
Ein Lehrer, der seinen Schülern beibringt, die Pumpenförderhöhe in mWS auszulegen, trägt die volle Verantwortung, wenn die Pumpen untauglich falsch dimensioniert werden. Für Heizungen sind sie dann nämlich erheblich zu groß, für die Wasserversorgung zu klein ausgelegt.
3.3 Formelzeichen der Achse
Im Kennliniendiagramm einer Pumpe ist das Formelzeichen H für die Förderhöhe richtig. Das wurde im vorausgegangenen Abschnitt verdeutlicht. Davon wird überhaupt nicht berührt, daß Rohrnetzberechnungen mit Dp durchgeführt werden. Es besteht auch kein Grund, die bisher durchgehend verwendete Bezeichnung "Förderhöhe" zu verändern.
4. Schlußbetrachtungen
Es war die Absicht, für die in der Einleitung beschriebenen Begriffe eine Klarheit der Definition herbeizuführen. Das konnte nicht gelingen. Denn zwei deutsche DIN-Normen, beide mit recht jungem Erscheinungsdatum, lassen unterschiedliche Beschreibungen für gleiche Begriffe zu. Nur die Ermittlung einer der beiden hydraulischen Einflußgrößen, nämlich die des Förderstroms, wird durch die Normung abgedeckt. Die Förderhöhe einer Heizungsumwälzpumpe ist nicht normgemäß berechenbar. So bleibt die Erkenntnis, daß es derzeit keine souveräne Lösung für die angesprochenen Probleme gibt. Andererseits sollte die Einsicht gewachsen sein, daß es zwecklos ist, eine und nur die eine Meinung gegen andere durchsetzen zu wollen.
Ein Beitrag aus einer diesbezüglichen Diskussion sei abschließend zitiert:
Welche Achsenbeschriftung letztendlich für Diagramme Verwendung findet, ist fast gleichgültig. Sie muß in der Wortwahl und als Zahlenwert handhabbar sein, als Dimension die physikalischen Zusammenhänge technisch präzise ausdrücken und dann natürlich noch von allen Beteiligten akzeptiert werden. Letzteres dürfte sicherlich das am schwierigsten zu erfüllende Kriterium sein.
L i t e r a t u r :
[1] Krist, Thomas: Neue internationale Einheiten der Technik und Physik, 1973.
[2] DIN 1301, Ausg. 11/1971: Einheiten, Einheitennamen, Einheitenzeichen.
[3] DIN 24260 Teil 1, Ausg. 09/1986: Flüssigkeitspumpen, Kreiselpumpen und Kreiselpumpenanlagen, Begriffe, Formelzeichen, Einheiten.
[4] DIN 1988, Ausg. 12/1988: Technische Regeln für Trinkwasser-Installationen (TRWI);
Teil 3: Ermittlung der Rohrdurchmesser,
Teil 5: Druckerhöhung und Druckminderung.
B i l d e r , wenn nicht extra angegeben: Wilo GmbH
[Zurück] [Übersicht] [www.ikz.de]